PAPER: The Principled Control of False Positives in Neuroimaging
– Current Citation:
Bennett CM, Wolford GL, Miller MB. (in press). The Principled Control of False Positives in Neuroimaging. Social Cognitive and Affective Neuroscience.
– Abstract:
An incredible amount of data is generated in the course of a functional neuroimaging experiment. The quantity of data gives us improved temporal and spatial resolution with which to evaluate our results. It also creates a staggering multiple testing problem. A number of methods have been created that address the multiple testing problem in neuroimaging in a principled fashion. These methods place limits on either the familywise error rate (FWER) or the false discovery rate (FDR) of the results. These principled approaches are well established in the literature and are known to properly limit the amount of false positives across the whole brain. However, a minority of papers are still published every month using methods that are improperly corrected for the number of tests conducted. These latter methods place limits on the voxelwise probability of a false positive and yield no information on the global rate of false positives in the results. In this commentary we argue in favor of a principled approach to the multiple testing problem – one that places appropriate limits on the rate of false positives across the whole brain and gives the reader the information they need to properly evaluate the results.
– Downloadable Versions:
[Manuscript PDF]
[Link to Journal PDF]
– Full Text:
The struggle between the appropriate treatment of false positives and false negatives is a fine line that every scientist must walk. If our criteria are too conservative we will not have the power to detect meaningful results. If our thresholds are too liberal our results will become contaminated by an excess of false positives. Ideally, we hope to maximize the number of true positives (hits) while minimizing false reports.
It is a statistical necessity that we must adapt our threshold criteria to the number of statistical tests completed on the same dataset. This multiple testing problem is not unique to neuroimaging; it affects many areas of modern science. Ask an economist about finding market correlations between 10,000 stocks or a geneticist about testing across 100,000 SNPs and you will quickly understand the pervasiveness of the multiple testing problem throughout scientific research (Storey and Tibshirani 2003; Taleb 2004).
In this paper we argue for the use of principled corrections when dealing with the large number of comparisons typical of neuroimaging data. By principled, we mean a correction that definitively identifies for the reader the probability or the proportion of false positives that could be expected in the reported results. Ideally, the correction would be easy for the reader to understand. Many researchers have avoided principled correction due to the perception that such methods are too conservative. In theory and in practice, there is no reason for a principled correction to be either liberal or conservative. The degree of ‘conservativeness’ generally can be adjusted by setting a parameter, maintaining accurate knowledge about the prevalence of false positives. Later in the commentary, we will outline familywise error rate correction (FWER) and false discovery rate correction (FDR) as two examples of principled correction.
The Problem
Many published fMRI papers use arbitrary, uncorrected statistical thresholds. A commonly chosen threshold is p < 0.001 with a minimum voxel clustering value of 10 voxels. For a few datasets this threshold may strike an appropriate balance between sensitivity and specificity; and in a few cases it might be possible to specify the probability of a false positive with this threshold. However, this uncorrected cutoff cannot be valid for the diverse array of situations in which it is used. The same threshold has been used with data comprising 10,000 voxels and with data comprising 60,000 voxels – this simply cannot be appropriate. The two situations have very different probabilities of false positives. The use of a principled procedure would yield the same expected probability or proportion of false positives for any number of voxels under investigation. In a recent survey of all articles published in six major neuroimaging journals during the year 2008 we found that between 25-30% of fMRI articles in each journal used uncorrected thresholds in their analysis (Bennett, Baird et al. Under Review). This percentage speaks to the fact that the majority of published research uses principled correction. However, the meta-analysis also highlights that a quarter to a third of published papers do not use principled correction, and that such papers continue to be published in high-impact, specialized journals. The proportion of studies using uncorrected thresholds is even higher within the realm of conference posters and presentations. In a survey of posters presented at a recent neuroscience conference we found that 80% of the presentations used uncorrected thresholds. In these unprincipled cases the reader is unlikely to have an accurate idea about the true likelihood of false positives in the results. The prevalence of unprincipled correction in the literature is a serious issue. During an examination of familywise error correction methods in neuroimaging, Nichols and Hayasaka (2003) compared techniques that included Gaussian Random Field Theory, Bonferroni, FDR, Šidák, and permutation. They found that only 8 out of 11 fMRI and PET studies had any significant voxels after familywise correction had been completed, leaving three studies with no significant voxels at all. Based on this data it is quite likely that results comprised wholly of false positives are present in the current literature. Despite this fact new studies reporting uncorrected statistics are published every month. False positives can be costly in a number of ways. One example of the negative consequences of false positives can be illustrated in a study completed by one of the current authors (MBM) in graduate school. He conducted an fMRI study investigating differential activations between false memories and true memories using the Roediger and McDermott word paradigm (1995). At the same time Schacter and colleagues were conducting a PET study using the same approach. Using a liberal uncorrected threshold Schacter and colleagues found a few small regions of interest in the medial temporal lobe and superior temporal sulcus (Schacter, Reiman et al. 1996). In their own results Miller and colleagues found two very different small clusters in the frontal and parietal cortex. When the Miller et al. study was presented at the Society for Neuroscience conference (Miller, Erickson et al. 1996) it was made clear that multiple testing correction was necessary. None of the results survived correction and the study was never released, while the uncorrected Schacter results were published in a major neuroimaging journal. Since that time there has been a scattering of studies reporting different patterns of brain activations for false memories and for true memories. Virtually all of them have used uncorrected thresholds and have proven difficult to replicate. This situation raises two issues. The first issue is the amount of time and resources that have been spent trying to extend results that may never have existed in the first place. The second issue is the prevailing skewed view of the literature that brain activations can be reliably discerned between false and true memories because only reports with positive results will be published. Less rigorous control of Type I errors would not be so bad if inferences based on false positives were easily correctable. However, this does not seem to be the case within the current model of publication. If researchers failed to reproduce the results of a currently published study it would be quite difficult to disseminate their null findings. This forms one of the most profound differences between Type I and Type II error: false negatives are correctable in future publications while false positives are difficult to refute once established in the literature. This imbalance in the propagation of Type I and Type II errors contributes to an issue known as the ‘File Drawer Problem’ (Rosenthal 1979). This refers to the publication bias that ensues because the probability of a study being published is directly tied to the significance of a result. While presentation of null results is not unheard of (see Baker, Hutchinson, 2007) such publications are generally considered the exception and not the rule. Another important cautionary tale is our recent investigation of false positives during the acquisition of fMRI data from a dead Atlantic salmon (Bennett, Baird et al. 2009; Bennett, Baird et al. Under Review). Using standard acquisition, preprocessing, and analysis techniques we were able to show that active voxel clusters could be observed in the dead salmon’s brain when using uncorrected statistical thresholds. If any form of correction for multiple testing was applied these false positives were no longer present. While the dead salmon study can only speak to the role of principled correction in a single subject, we believe it effectively illustrates the dangers of false positives in any neuroimaging analysis. A bit of clarification may be important at this point. Our goal should not be to completely eliminate false positives. To be completely certain that all of our results are true positives would require obscenely high statistical thresholds that would eliminate all but the very strongest of our legitimate results. Therefore we must accept that there will always be some risk of false positives in our reports. At the same time, it is critical that we be able to specify how probable false positives are in our data in a way that is readily communicated to the reader. In this discussion of false positives it is also important that we not minimize the danger of high false negative rates. Being over-conservative regarding the control of Type I error comes at the expense of missing true positives. Perhaps for this reason there have been some voices in the imaging community that argue against principled correction due to the resulting loss of statistical power. Again, a principled correction does not necessarily lead to a loss of power. The researcher can set a liberal criterion in FDR or FWE and the readers can use their precise knowledge of the false positive rate to evaluate the reported results. Our Argument
There is a single key argument that we wish to make regarding proper protection against Type I error in fMRI. All researchers should use statistical methods that provide information on the Type I error rate across the whole brain. It doesn’t matter what method you use to accomplish this. You can report the false discovery rate (Benjamini and Hochberg 1995), or use one of several methods to control for the familywise error rate (Nichols and Hayasaka 2003). You can even do a back-of-the-napkin calculation and use a Bonferroni-corrected threshold if you wish. The end goal is the same: giving the reader information on the prevalence of false positives across the entire family of statistical tests.
We would further argue that an investigator could still use an uncorrected threshold for their data as long as proper corrected values detailing the prevalence of false positives are also provided. In this manner you could threshold your data at p < 0.001 with a 10 voxel extent as long as you presented what FDR or FWE threshold would be required for the results to stay significant. One example can be seen in the above figure. In this image voxels that survive an uncorrected threshold are depicted in cool colors while voxels that survive FDR correction are depicted in warm colors. This allows a researcher to ‘have their cake and eat it too’. Again, the key to our argument is not that we need to use correction simply for correction’s sake, just that our readers are made aware of the false positive rate across the whole brain. Techniques For Principled Correction
There are a wide variety of methods that can be used to hold the false positive rate at specified levels across the whole brain. One approach is to place limits on the familywise error rate (FWER). Using this method a criterion value of 0.05 would mean that there is a 5% chance of one or more false positives across the entire set of tests. This yields a 95% confidence level that there are no false positives in your results. There are many methods that can be used to control the FWER in neuroimaging data: the Bonferroni correction, the use of Gaussian Random Field Theory (Worsley, Evans et al. 1992), and nonparametric permutation correction techniques (Nichols and Holmes 2002). Nichols and Hayasaka (2003) have authored an excellent article reviewing these techniques. The Bonferroni correction is typically seen as too conservative for functional neuroimaging since it does not take into account spatial correlation between voxels. Gaussian RFT adapts to spatial smoothness of the data, but was shown to be quite conservative at low levels of smoothness. The use of permutation-based techniques to control the FWER emerged as an ideal choice for adequate correction while maintaining high sensitivity.
Another approach to principled correction is to place limits on the false discovery rate (Benjamini and Hochberg 1995; Genovese, Lazar et al. 2002). Using this method a criterion value of 0.05 would mean that on average 5% of the observed results would be false positives. The goal of this approach is not to completely eliminate familywise errors, but to control how pervasive false positives are in the results. This is a weaker control to the multiple testing problem, but one that still provides precise estimates of the percentage of false positives.
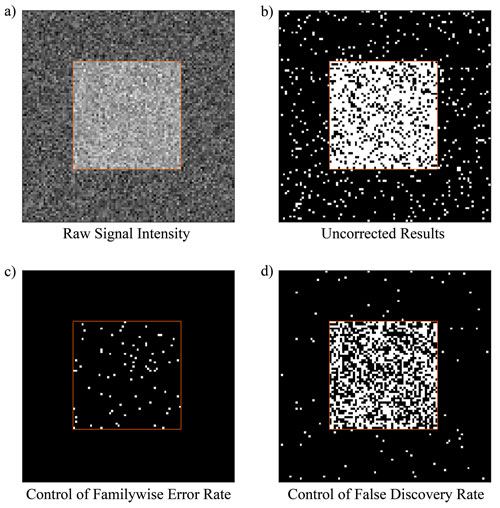
The advantages and disadvantages of each correction approach are illustrated graphically using simulated data in Figure 2. The simulated data is set up so that the uncorrected results have a power of 0.80. Controlling for the familywise error rate with the criterion p(FWE) = 0.05 can be seen to virtually eliminate false positives while dramatically reducing the amount of detected signal. In this example power is reduced to 0.16. Controlling the false discovery rate with the criterion FDR = 0.05 increases the number of false positives relative to FWER techniques, but also increases the ability to detect meaningful signal. In this example power is increased to 0.54.
If you are concerned about power, you can appropriately adjust the cutoff in FWE or FDR. For instance, it isn’t strictly necessary to use 0.05 in either FWE or FDR. It might yield a better balance of power and false positive protection to use 0.10 or even something higher. You will be more likely to find true sources of activation and the reader will still have a precise idea about the prevalence of false positives.
It is important to understand the appropriate use of the correction method you select. For instance, one commonly used approach is the small-volume correction (SVC) method in SPM (http://www.fil.ion.ucl.ac.uk/spm/). The use of SVC allows researchers to conduct principled correction using Gaussian Random Field Theory within a predefined region of interest. Ideally this would be a region defined by anatomical boundaries or a region identified in a previous, independent dataset. However, many researchers implement SVC incorrectly, choosing to first conduct a whole-brain exploratory analysis and then using SVC on the resulting clusters (cf. Loring, Meador et al. 2002; Poldrack and Mumford 2009). This is an inappropriate approach that does not yield a principled correction. Another method that is often incorrectly used is the AlphaSim tool included in AFNI (http://afni.nimh.nih.gov/afni/). For effective false positive control AlphaSim requires that an estimate of the spatial correlation across voxels be modeled using the program 3dFWHM. Many researchers simply input the amount of Gaussian smoothing that was applied during preprocessing, leading to incorrect clustering thresholds as output. Errors during estimation of the spatial smoothness can also lead to incorrect values.
In the future we may have statistical methods that are better able to address the multiple testing problem. Hierarchical Bayes models have been offered as one approach (Lindquist and Gelman 2009). We may even move away from the binary decision of significance and begin to examine effect sizes in earnest (Wager 2009). Still, we must examine the balance of Type I and Type II error in the context of where our analysis techniques are today. At present the general linear model is by far the most prevalent method of analysis in fMRI. Mumford and Nichols (2009) found that approximately 92% of group fMRI results were computed using an ordinary least squares (OLS) estimation of the general linear model. This percentage is unlikely to shift dramatically in the next 12-36 months. Our focus should remain on how to improve OLS methods in the near term as we move toward new analysis techniques in the future.
Predetermined cluster size as a partial correction
In neuroimaging we often rely on the fact that legitimate results tend to spatially cluster together. The assumption being that voxel clustering provides some assurance against Type I errors. While predefined thresholds in combination with predetermined clustering requirements may represent a sufficient approximation of a proper threshold, it is in general an unprincipled approach to the control of Type I error rates.
Many authors justify this approach by referring to the results of Forman et al. (1995), who examined clustering behavior of voxels in fMRI. The results of Forman et al. suggest that a threshold of p < 0.001 combined with a 10 voxel extent requirement should more than adequately control for the prevalence of false positives. However, the Forman et al. data was only computed across two-dimensional slices, not in 3D volumes. The findings of Forman et al. simply do not apply to modern fMRI data. It should also be noted that we are not arguing that p < 0.001 with a 10 voxel threshold is wholly inappropriate. For example, Cooper and Knutson (2008) used the AlphaSim utility in AFNI to determine that a corrected threshold of p < 0.001 with a 10 voxel extent threshold would be appropriate to keep the familywise error rate at 5% in their particular dataset. The problem is that this threshold is specific to the parameters of their dataset, and may be inappropriate in other datasets. Arnott et al. (2008) used the same AFNI routine and estimated that an 81 voxel extent was required to ensure that familywise error was kept below 5%. It is possible to use the combination of a p value and a cluster size in a principled way, but it requires computing the proper values for each and every analysis. The cluster size criteria can change quite substantially from dataset to dataset. Further, it can be the case that required cluster sizes become so large that legitimate results with a smaller volume are missed. Conclusions
The topic of proper Type I error protection is not a new element of discussion in the field of neuroimaging. The need to correct for thousands of statistical tests has been recognized since the early PET imaging days (Worsley, Evans et al. 1992). It is uncertain why uncorrected thresholds have lingered so long. Perhaps many researchers simply recognized it as an accepted, arbitrary threshold in the same manner p < 0.05 is an accepted, arbitrary threshold throughout other scientific fields. This approach may have been acceptable in the past, but within the last decade we, as a field, have come under increased scrutiny from the public and from other scientists. At a time when so many are looking for us to slip up we believe it is time to set a new standard of quality with regard to our data acquisition and analysis. The fundamental question that that all researchers must face is whether their results will replicate in a new study. The prevalence of false positives in your results will directly influence this ability. We are all aware that the multiple testing problem is a major issue in neuroimaging. How you correct for this problem can be debated, but principled protection against Type I error is an absolute necessity moving forward. References
Arnott, S. R., J. S. Cant, et al. (2008). “Crinkling and crumpling: an auditory fMRI study of material properties.” Neuroimage 43(2): 368-78.
Benjamini, Y. and Y. Hochberg (1995). “Controlling the false discovery rate: A practical and powerful approach to multiple testing.” J. Roy. Statist. Soc. Ser. B 57: 289-300.
Bennett, C. M., A. A. Baird, et al. (2009). Neural Correlates of Interspecies Perspective Taking in the Post-Mortem Atlantic Salmon: An Argument For Proper Multiple Comparisons Correction 15th Annual Meeting of the Organization for Human Brain Mapping. San Francisco, CA.
Bennett, C. M., A. A. Baird, et al. (Under Review). “Neural Correlates of Interspecies Perspective Taking in the Post-Mortem Atlantic Salmon: An Argument For Proper Multiple Comparisons Correction “.
Cooper, J. C. and B. Knutson (2008). “Valence and salience contribute to nucleus accumbens activation.” Neuroimage 39(1): 538-47.
Forman, S. D., J. D. Cohen, et al. (1995). “Improved assessment of significant activation in functional magnetic resonance imaging (fMRI): use of a cluster-size threshold.” Magn Reson Med 33(5): 636-47.
Genovese, C. R., N. A. Lazar, et al. (2002). “Thresholding of statistical maps in functional neuroimaging using the false discovery rate.” Neuroimage 15(4): 870-8.
Lindquist, M. A. and A. Gelman (2009). “Correlations and Multiple Comparisons in Functional Imaging: A Statistical Perspective (Commentary on Vul et al., 2009).” Perspectives on Psychological Science 4(3): 310-313.
Loring, D. W., K. J. Meador, et al. (2002). “Now you see it, now you don’t: statistical and methodological considerations in fMRI.” Epilepsy Behav 3(6): 539-547.
Miller, E. K., C. A. Erickson, et al. (1996). “Neural mechanisms of visual working memory in prefrontal cortex of the macaque.” J Neurosci 16(16): 5154-67.
Mumford, J. A. and T. Nichols (2009). “Simple group fMRI modeling and inference.” Neuroimage 47(4): 1469-75.
Nichols, T. and S. Hayasaka (2003). “Controlling the familywise error rate in functional neuroimaging: a comparative review.” Stat Methods Med Res 12(5): 419-46.
Nichols, T. E. and A. P. Holmes (2002). “Nonparametric permutation tests for functional neuroimaging: a primer with examples.” Hum Brain Mapp 15(1): 1-25.
Poldrack, R. A. and J. A. Mumford (2009). “Independence in ROI analysis: where is the voodoo?” Soc Cogn Affect Neurosci 4(2): 208-13.
Roediger, H. L., 3rd and K. B. McDermott (1995). “Creating false memories: remembering words not presented in lists.” Journal of Experimental Psychology: Learning, Memory, and Cognition 21: 803-814.
Rosenthal, R. (1979). “The file drawer problem and tolerance for null results.” Psychological Bulletin 83(3): 638-641.
Schacter, D. L., E. Reiman, et al. (1996). “Neuroanatomical correlates of veridical and illusory recognition memory: evidence from positron emission tomography.” Neuron 17(2): 267-74.
Storey, J. D. and R. Tibshirani (2003). “Statistical significance for genomewide studies.” Proc Natl Acad Sci U S A 100(16): 9440-5.
Taleb, N. (2004). Fooled by randomness: the hidden role of chance in lafe and in the market. New York, Thompson/Texere.
Wager, T. D. (2009). If neuroimaging is the answer, what is the question? Estimating Effects and Correlations in Neuroimaging Data Workshop, Columbia University, New York, NY.
Worsley, K. J., A. C. Evans, et al. (1992). “A three-dimensional statistical analysis for CBF activation studies in human brain.” Journal of Cerebral Blood Flow & Metabolism 12(6): 900-918.

Leave a Reply
You must be logged in to post a comment.