The Middle Ground in Multiple Comparisons Correction
I got a note last week from a longtime colleague seeking advice on some reviewer comments of their latest paper. In their remarks the reviewer requested that the authors revert the corrected statistical threshold back to an uncorrected level of p < 0.001. The authors were left scratching their heads, wondering how they were going to justify their use of a standard statistical technique. I was a bit shocked to hear that the reviewer was so opposed to multiple comparisons correction, but not entirely surprised. As multiple comparisons correction has become increasingly standard there seems to be a subtle push against it from some in the neuroimaging field. We experienced the push ourselves when we got our first rejection on the fish paper. The reviewer said that there needed to be a more in-depth discussion of avoiding both Type I and Type II error in the paper. They added that always controlling for multiple comparisons correction could potentially lead one to ignore legitimate results that fall short of the corrected statistic value.
So, as a researcher, what do you value more? Do you want to ensure that false positives are controlled, or do you want to minimize false negatives? Do you side with roughly 80% of the field and correct for multiple comparisons, guarding against Type I error, or do you side with the other 20% of the field and use uncorrected stats, minimizing the chance of Type II error? [1]
My position: why not do both?
For the last two years I have been an advocate of reporting both uncorrected and corrected statistics in results tables and figures. It just makes sense. An example of this approach is posted below, shown as corrected results overlaid on top of uncorrected results for an inflated cortical surface. Regions surviving an uncorrected threshold of p < 0.001 with an 8 voxel extent threshold are shown in blue and the subset of regions surviving a FDR-corrected threshold of p(FDR) = 0.05 with an 8 voxel extent threshold are shown in yellow/orange.
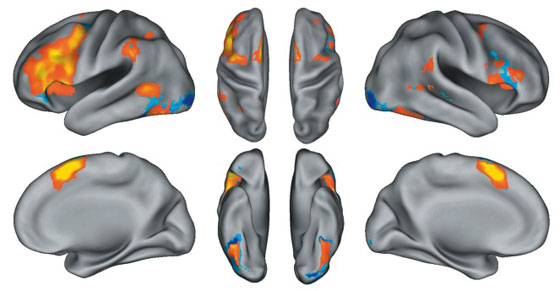
At a glance you can see what regions survive multiple comparisons correction and which only survive an uncorrected threshold. Most interesting to me is that, for this task, there are some regions that survive an uncorrected threshold but do not survive the FDR threshold. For example, the left and right occipital pole in both hemispheres is only significant for uncorrected statistic values.
In writing the paper for the above data we have refrained from discussing the regions that do not survive multiple comparisons correction. Still, what I consider elegant is that I can give the reader additional information about the data from which they can make their own judgements. Perhaps a vision researcher would be interested in the uncorrected result and could run a more powerful study to investigate this effect, who knows. The point is that our readers, by and large, are very smart people. I don’t mind giving them all the information I can for them to draw their own conclusions and insights from. I also think that it represents a very good balance between those who support multiple comparisons correction and those who, as my colleague encountered, insist on uncorrected thresholds.
[1] – Stats gathered during a forthcoming literature review in the salmon paper.
3 Responses to “The Middle Ground in Multiple Comparisons Correction”
What a dead salmon reminds us about fMRI analysis « Stanford Center for Law & the Biosciences Blog - September 18th, 2009
[…] some researchers think it may be overly conservative and thus miss true positives. As a solution, Bennett suggests reporting both sets of data, corrected and […]
Law and Biosciences Blog | What a dead salmon reminds us about fMRI analysis - June 1st, 2010
[…] some researchers think it may be overly conservative and thus miss true positives. As a solution, Bennett suggests reporting both sets of data, corrected and […]
fMRI Gets Slap in the Face with a Dead Fish | Brain and Head Health - April 2nd, 2012
[…] throwing the baby salmon out with the bathwater, as it were. This is a legitimate point, but as Bennett says, in this case we should report both corrected and uncorrected results, to make it clear to the […]
Leave a Reply
You must be logged in to post a comment.